
Numim graficul unei funcții f: A → B mulțimea
Gf = {(a, f(a)) ∈ A × B │ a ∈ A}.
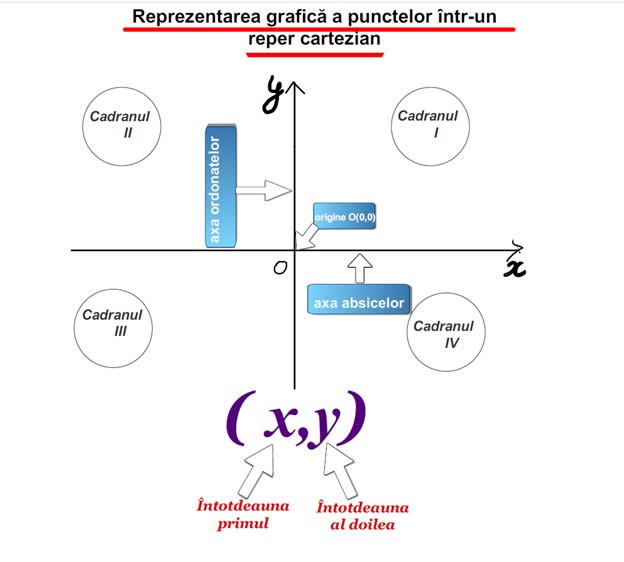
Dacă f este o funcție numerică (adică A, B ⊂ ℝ), atunci Gf are o reprezentare geometrică într-un plan pentru care am ales un reper cartezian. Această reprezentare geometrică se numește, de obicei, tot graficul funcției f.
Imaginea funcției f: A → B este mulțimea
Im f = {y ∈ B │ (∃) x ∈ A pentru care f(x) = y} ⊂ B.
Funcția f: A → B este injectivă dacă:
∀ x, y ∈ A, x ≠ y ⟹ f(x) ≠ f(y) sau ∀ x, y ∈ A, f(x) = f(y) ⟹ x = y
Funcția f: A → B este surjectivă dacă:
Im f = B, adică ∀ y ∈ B, (∃) x ∈ A, pentru care f(x) = y.
O funcție se numește bijectivă dacă este atât injectivă cât și surjectivă.
Funcția f: D ⊂ ℝ → ℝ se numește funcție descrescătoare (strict descrescătoare)
dacă
∀ x1, x2 ∈ D, x1 < x2 ⟹ f(x1) ≥ f(x2)
(f(x1) > f(x2)).
Funcția f: D ⊂ ℝ → ℝ se numește funcție crescătoare (strict crescătoare) dacă
∀ x1, x2 ∈ D, x1 < x2 ⟹ f(x1) ≤ f(x2)
(f(x1) < f(x2)).
Funcția se numește monotonă (strict monotonă) dacă este sau crescătoare (strict crescătoare) sau descrescătoare (strict descrescătoare).
Dacă f: A → B și g: B → C sunt două funcții, compusa lor este
funcția g∘f: A → C definită prin
(g∘f)(x) = g(f(x)), ∀ x ∈ A.
Dacă notăm cu 1A: A → A, 1A (x) = x, ∀ x ∈ A funcția identică a
mulțimii A, atunci f∘1A = f, pentru orice
funcție f: A → B și 1A∘g = g, pentru orice funcție
g: C → A.
Funcția f: A → B se numește inversabilă dacă există g: B → A,
astfel încât f∘g = 1B. Dacă există, funcția g este
unică; ea se numește inversa lui f și se notează
f-1. Pentru x ∈ A și y ∈ B, are loc
relația
f(x) = y ⟺ f-1(y) = x.
O funcție este inversabilă dacă și numai dacă este bijectivă.
O funcție f: ℝ → ℝ se numește pară dacă
f(-x) = f(x). Graficul unei funcții pare este simetric față de axa
Oy.
O funcție f: ℝ → ℝ se numește impară dacă
f(-x) = -f(x). Graficul unei funcții impare este simetric față de
originea sistemului de coordonate.
O funcție f: ℝ → ℝ se numește periodică dacă există un număr
T ∈ ℝ^* (numit perioadă a lui f) astfel încât
f(x + T) = f(x). Cea mai mică perioadă strict pozitivă, dacă există,
se numește perioadă principală a lui f.